DRS Example#
This code tests the proof of Douglas–Rachford splitting methods, introduced in Proposition 3.1 of “Exact worst-case convergence rates for Douglas–Rachford and Davis–Yin splitting methods” by Edward Duc Hien Nguyen, Jaewook J. Suh, Xin Jiang, Shiqian Ma (2025).
The implementation in terms of the PEP is based on the PDHG implementation done in the paper “Interpolation Conditions for Linear Operators and Applications to Performance Estimation Problems” by Nizar Bousselmi, Julien M. Hendrickx, François Glineur (2023).
Import the required libraries#
import pepflow as pf
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
import itertools
from IPython.display import display
Define the functions#
f = pf.ConvexFunction(is_basis=True, tags=["f"])
g = pf.ConvexFunction(is_basis=True, tags=["g"])
h = (f + g).add_tag("h")
Write a function to return the PEPContext associated with DRS#
def make_ctx_drs(
ctx_name: str, N: int | sp.Integer, stepsize: pf.Parameter
) -> pf.PEPContext:
ctx_drs = pf.PEPContext(ctx_name).set_as_current()
# Declare the initial points.
x_0 = pf.Vector(is_basis=True, tags=["x_0"])
u_0 = pf.Vector(is_basis=True, tags=["u_0"])
# Declare the points used in the primal-dual gap function.
_ = pf.Vector(is_basis=True, tags=["x_{{tilde}}"]) # ty: ignore
u_tilde = pf.Vector(is_basis=True, tags=["u_{{tilde}}"])
# Moving Average
x_sum = pf.Vector.zero()
u_sum = pf.Vector.zero()
x = x_0
u = u_0
for i in range(N):
x_old = x
x = f.prox(x - stepsize * u, stepsize, tag=f"x_{i + 1}")
t = u + 1 / stepsize * (2 * x - x_old)
p = g.prox(stepsize * t, stepsize, tag=f"p_{i + 1}")
u = t - 1 / stepsize * p
u.add_tag(f"u_{i + 1}")
x_sum = x_sum + x
u_sum = u_sum + u
_ = (x_sum / float(N)).add_tag("x_{{avg}}") # ty: ignore
u_avg = (u_sum / float(N)).add_tag("u_{{avg}}")
# Define p_tilde and p_avg such that u_tilde \in \partial g(p_tilde) and u_avg \in \partial g(u_avg)
p_tilde = pf.Vector(is_basis=True, tags=["p_{{tilde}}"])
p_avg = pf.Vector(is_basis=True, tags=["p_{{avg}}"])
g.add_point_with_grad_restriction(p_tilde, u_tilde)
g.add_point_with_grad_restriction(p_avg, u_avg)
return ctx_drs
Write a function to return the PEPBuilder for DRS#
def make_pb_drs(
ctx: pf.PEPContext, stepsize: pf.Parameter, init_distance: pf.Parameter
) -> pf.PEPBuilder:
x_0 = ctx["x_0"]
x_tilde = ctx["x_{{tilde}}"]
x_avg = ctx["x_{{avg}}"]
u_0 = ctx["u_0"]
u_tilde = ctx["u_{{tilde}}"]
u_avg = ctx["u_{{avg}}"]
p_tilde = ctx["p_{{tilde}}"]
p_avg = ctx["p_{{avg}}"]
pb = pf.PEPBuilder(ctx_plt)
# Initial Condition
pb.add_initial_constraint(
((1.0 / stepsize) * (x_0 - x_tilde) ** 2 + stepsize * (u_0 - u_tilde) ** 2).le(
init_distance, name="initial_condition"
)
)
# Set performance metric of primal-dual gap function
pb.set_performance_metric(
f(x_avg)
- f(x_tilde)
+ g(p_tilde)
- g(p_avg)
+ u_tilde * x_avg
- u_tilde * p_tilde
- u_avg * x_tilde
+ u_avg * p_avg
)
return pb
Numerical evidence of convergence of DRS#
N = 8
alpha = pf.Parameter("alpha")
R = pf.Parameter("R")
alpha_value = 1
R_value = 1
opt_values = []
for k in range(1, N):
ctx_plt = make_ctx_drs(ctx_name=f"ctx_plt_{k}", N=k, stepsize=alpha)
pb_plt = make_pb_drs(ctx_plt, alpha, R)
result = pb_plt.solve(resolve_parameters={"alpha": alpha_value, "R": R_value})
opt_values.append(result.opt_value)
iters = np.arange(1, N)
cont_iters = np.arange(1, N, 0.01)
plt.plot(
cont_iters,
1 / (cont_iters + 1),
"r-",
label="Analytical bound $\\frac{1}{k+1}$",
)
plt.scatter(iters, opt_values, color="blue", marker="o", label="Numerical values")
plt.legend()
<matplotlib.legend.Legend at 0x7f6472d645d0>
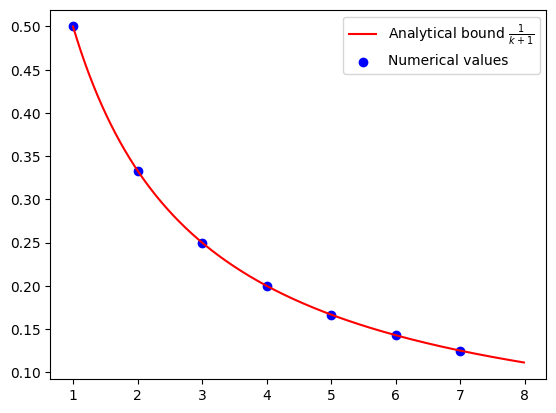
Verification of convergence of DRS#
N = sp.S(2)
alpha_value = sp.S(1)
R_value = sp.S(1)
ctx_prf = make_ctx_drs(ctx_name="ctx_prf", N=N, stepsize=alpha)
pb_prf = make_pb_drs(ctx_prf, alpha, R)
result = pb_prf.solve(resolve_parameters={"alpha": alpha_value, "R": R_value})
print(result.opt_value)
# Dual variables associated with the interpolations conditions of f with no relaxation
lamb_dense = result.get_scalar_constraint_dual_value_in_numpy(f)
# Dual variables associated with the interpolations conditions of g with no relaxation
gamm_dense = result.get_scalar_constraint_dual_value_in_numpy(g)
0.33333237948624217
pf.launch_primal_interactive(
pb_prf, ctx_prf, resolve_parameters={"alpha": alpha_value, "R": R_value}
)
Dash app running on http://127.0.0.1:8050/
Solve the problem again with the found relaxation#
def tag_to_index(tag, N=N):
"""This is a function that takes in a tag of an iterate and returns its index.
We index "x_{n} as "n-1".
We index "x_avg" as "N" where N is the last iterate.
We index "x_tilde" as "N+1" where N is the last iterate.
"""
# Split the string on "_" and get the index
if (idx := tag.split("_")[1]).isdigit():
return int(idx) - 1
elif idx == "{{avg}}":
return N
elif idx == "{{tilde}}":
return N + 1
relaxed_constraints = []
for tag_i in lamb_dense.row_names:
i = tag_to_index(tag_i)
for tag_j in lamb_dense.col_names:
j = tag_to_index(tag_j)
if i == N + 1 and j in range(N):
continue
if i in range(N) and j == N:
continue
relaxed_constraints.append(f"f:{tag_i},{tag_j}")
for tag_i in gamm_dense.row_names:
i = tag_to_index(tag_i)
for tag_j in gamm_dense.col_names:
j = tag_to_index(tag_j)
if i == N and j in range(N):
continue
if i in range(N) and j == N + 1:
continue
relaxed_constraints.append(f"g:{tag_i},{tag_j}")
pb_prf.set_relaxed_constraints(relaxed_constraints)
result = pb_prf.solve(resolve_parameters={"alpha": alpha_value, "R": R_value})
# Dual variable associated with the initial condition
tau_sol = result.dual_var_manager.dual_value("initial_condition")
# Dual variable associated with the interpolations conditions of f
lamb_sol = result.get_scalar_constraint_dual_value_in_numpy(f)
# Dual variable associated with the interpolations conditions of g
gamm_sol = result.get_scalar_constraint_dual_value_in_numpy(g)
# Dual variable associated with the Gram matrix G
S_sol = result.get_gram_dual_matrix()
Verify closed form expression of \(\lambda\)#
Print the values of \(\lambda\) obtained from the solver
lamb_sol.pprint()
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccc}
& x_1 & x_2 & x_{{avg}} & x_{{tilde}} \\
\hline
x_1 & 0.0 & 0.0 & 0.5 & 0.0 \\x_2 & 0.0 & 0.0 & 0.5 & 0.0 \\x_{{avg}} & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & 0.5 & 0.5 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
def lamb(tag_i, tag_j, N=N):
i = tag_to_index(tag_i)
j = tag_to_index(tag_j)
if i == N + 1 and j in range(N):
return 1 / N
if i in range(N) and j == N:
return 1 / N
return 0
lamb_cand = pf.pprint_labeled_matrix(
lamb, lamb_sol.row_names, lamb_sol.col_names, return_matrix=True
)
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccc}
& x_1 & x_2 & x_{{avg}} & x_{{tilde}} \\
\hline
x_1 & 0.0 & 0.0 & 0.5 & 0.0 \\x_2 & 0.0 & 0.0 & 0.5 & 0.0 \\x_{{avg}} & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & 0.5 & 0.5 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
Check whether our candidate of \(\lambda\) matches with solution
print(
"Did we guess the right closed form of lambda?",
np.allclose(lamb_cand, lamb_sol.matrix, atol=1e-4),
)
Did we guess the right closed form of lambda? True
Verify closed form expression of \(\gamma\)#
Print the values of \(\gamma\) obtained from the solver
gamm_sol.pprint()
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccc}
& p_1 & p_2 & p_{{avg}} & p_{{tilde}} \\
\hline
p_1 & 0.0 & 0.0 & 0.0 & 0.5 \\p_2 & 0.0 & 0.0 & 0.0 & 0.5 \\p_{{avg}} & 0.5 & 0.5 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
# We consider proper shifting since x_0 is not in the gamma matrix
def gamm(tag_i, tag_j, N=N):
i = tag_to_index(tag_i)
j = tag_to_index(tag_j)
if i == N and j in range(N):
return 1 / N
if i in range(N) and j == N + 1:
return 1 / N
return 0
gamm_cand = pf.pprint_labeled_matrix(
gamm, gamm_sol.row_names, gamm_sol.col_names, return_matrix=True
)
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccc}
& p_1 & p_2 & p_{{avg}} & p_{{tilde}} \\
\hline
p_1 & 0.0 & 0.0 & 0.0 & 0.5 \\p_2 & 0.0 & 0.0 & 0.0 & 0.5 \\p_{{avg}} & 0.5 & 0.5 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
print(
"Did we guess the right closed form of gamma?",
np.allclose(gamm_sol.matrix, gamm_cand, atol=1e-4),
)
Did we guess the right closed form of gamma? True
Verify closed form expression \(S\)#
Create an ExpressionManager to translate \(x_i\), \(f(x_i)\), and \(\nabla f(x_i)\) into a basis representation
pm = pf.ExpressionManager(
ctx_prf, resolve_parameters={"alpha": alpha_value, "R": R_value}
)
Print the values of \(S\) obtained from the solver
S_sol.pprint()
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccccccccccc}
& x_0 & u_0 & x_{{tilde}} & u_{{tilde}} & \nabla f(x_1) & \nabla g(p_1) & \nabla f(x_2) & \nabla g(p_2) & p_{{tilde}} & p_{{avg}} & \nabla f(x_{{avg}}) & \nabla f(x_{{tilde}}) \\
\hline
x_0 & 0.333 & 0.0 & -0.333 & -0.0 & -0.25 & -0.25 & -0.25 & -0.25 & 0.0 & 0.0 & -0.0 & 0.0 \\u_0 & 0.0 & 0.333 & -0.0 & -0.333 & 0.25 & 0.25 & 0.25 & 0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & -0.333 & -0.0 & 0.333 & 0.0 & 0.25 & 0.25 & 0.25 & 0.25 & -0.0 & -0.0 & 0.0 & 0.0 \\u_{{tilde}} & -0.0 & -0.333 & 0.0 & 0.333 & -0.25 & -0.25 & -0.25 & -0.25 & -0.0 & -0.0 & -0.0 & 0.0 \\\nabla f(x_1) & -0.25 & 0.25 & 0.25 & -0.25 & 0.5 & 0.5 & 0.25 & 0.25 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla g(p_1) & -0.25 & 0.25 & 0.25 & -0.25 & 0.5 & 0.5 & 0.25 & 0.25 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_2) & -0.25 & 0.25 & 0.25 & -0.25 & 0.25 & 0.25 & 0.5 & 0.5 & 0.0 & -0.0 & 0.0 & 0.0 \\\nabla g(p_2) & -0.25 & 0.25 & 0.25 & -0.25 & 0.25 & 0.25 & 0.5 & 0.5 & 0.0 & -0.0 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 \\p_{{avg}} & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_{{avg}}) & -0.0 & 0.0 & 0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 & -0.0 & 0.0 \\\nabla f(x_{{tilde}}) & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
Subtract the decomposed closed-form expressions
x = ctx_prf.tracked_point(f)
p = ctx_prf.tracked_point(g)
u = [ctx_prf[f"u_{i}"] for i in range(1, N + 1)]
v = [f.grad(x[i]) + u[i] for i in range(N)]
x_0 = ctx_prf["x_0"]
x_tilde = ctx_prf["x_{{tilde}}"]
u_0 = ctx_prf["u_0"]
u_tilde = ctx_prf["u_{{tilde}}"]
print(x)
print(p)
print(u)
[x_1, x_2, x_{{avg}}, x_{{tilde}}]
[p_1, p_2, p_{{avg}}, p_{{tilde}}]
[u_1, u_2]
S_guess1_x = (
1
/ (alpha * (N + 1))
* (x_0 - x_tilde - alpha * (N + 1) / (2 * N) * sum(v[i] for i in range(N))) ** 2
)
S_guess1_u = (
alpha
/ (N + 1)
* (u_0 - u_tilde + (N + 1) / (2 * N) * sum(v[i] for i in range(N))) ** 2
)
remainder1 = S_sol.matrix - pm.eval_scalar(S_guess1_x + S_guess1_u).inner_prod_coords
pf.pprint_labeled_matrix(remainder1, S_sol.row_names, S_sol.col_names)
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccccccccccc}
& x_0 & u_0 & x_{{tilde}} & u_{{tilde}} & \nabla f(x_1) & \nabla g(p_1) & \nabla f(x_2) & \nabla g(p_2) & p_{{tilde}} & p_{{avg}} & \nabla f(x_{{avg}}) & \nabla f(x_{{tilde}}) \\
\hline
x_0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 \\u_0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 \\u_{{tilde}} & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 \\\nabla f(x_1) & -0.0 & 0.0 & 0.0 & -0.0 & 0.125 & 0.125 & -0.125 & -0.125 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla g(p_1) & -0.0 & 0.0 & 0.0 & -0.0 & 0.125 & 0.125 & -0.125 & -0.125 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_2) & 0.0 & -0.0 & -0.0 & 0.0 & -0.125 & -0.125 & 0.125 & 0.125 & 0.0 & -0.0 & 0.0 & 0.0 \\\nabla g(p_2) & 0.0 & -0.0 & 0.0 & 0.0 & -0.125 & -0.125 & 0.125 & 0.125 & 0.0 & -0.0 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 \\p_{{avg}} & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_{{avg}}) & -0.0 & 0.0 & 0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 & -0.0 & 0.0 \\\nabla f(x_{{tilde}}) & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
S_guess2 = (
alpha
/ (4 * N**2)
* sum((v[i] - v[j]) ** 2 for i, j in itertools.product(range(N), range(N)))
)
remainder2 = remainder1 - pm.eval_scalar(S_guess2).inner_prod_coords
pf.pprint_labeled_matrix(remainder2, S_sol.row_names, S_sol.col_names)
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccccccccccc}
& x_0 & u_0 & x_{{tilde}} & u_{{tilde}} & \nabla f(x_1) & \nabla g(p_1) & \nabla f(x_2) & \nabla g(p_2) & p_{{tilde}} & p_{{avg}} & \nabla f(x_{{avg}}) & \nabla f(x_{{tilde}}) \\
\hline
x_0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 \\u_0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 \\u_{{tilde}} & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 \\\nabla f(x_1) & -0.0 & 0.0 & 0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla g(p_1) & -0.0 & 0.0 & 0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_2) & 0.0 & -0.0 & -0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & -0.0 & 0.0 & 0.0 \\\nabla g(p_2) & 0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & -0.0 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 \\p_{{avg}} & 0.0 & 0.0 & -0.0 & -0.0 & 0.0 & 0.0 & -0.0 & -0.0 & -0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_{{avg}}) & -0.0 & 0.0 & 0.0 & -0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -0.0 & 0.0 & -0.0 & 0.0 \\\nabla f(x_{{tilde}}) & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
Check whether our candidate of \(S\) matches with solution
S_guess = S_guess1_x + S_guess1_u + S_guess2
S_guess_eval = pm.eval_scalar(S_guess).inner_prod_coords
pf.pprint_labeled_matrix(S_guess_eval, S_sol.row_names, S_sol.col_names)
\[\begin{split}\displaystyle \displaystyle
\begin{array}{c|cccccccccccc}
& x_0 & u_0 & x_{{tilde}} & u_{{tilde}} & \nabla f(x_1) & \nabla g(p_1) & \nabla f(x_2) & \nabla g(p_2) & p_{{tilde}} & p_{{avg}} & \nabla f(x_{{avg}}) & \nabla f(x_{{tilde}}) \\
\hline
x_0 & 0.333 & 0.0 & -0.333 & 0.0 & -0.25 & -0.25 & -0.25 & -0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\u_0 & 0.0 & 0.333 & 0.0 & -0.333 & 0.25 & 0.25 & 0.25 & 0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\x_{{tilde}} & -0.333 & 0.0 & 0.333 & 0.0 & 0.25 & 0.25 & 0.25 & 0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\u_{{tilde}} & 0.0 & -0.333 & 0.0 & 0.333 & -0.25 & -0.25 & -0.25 & -0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_1) & -0.25 & 0.25 & 0.25 & -0.25 & 0.5 & 0.5 & 0.25 & 0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla g(p_1) & -0.25 & 0.25 & 0.25 & -0.25 & 0.5 & 0.5 & 0.25 & 0.25 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_2) & -0.25 & 0.25 & 0.25 & -0.25 & 0.25 & 0.25 & 0.5 & 0.5 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla g(p_2) & -0.25 & 0.25 & 0.25 & -0.25 & 0.25 & 0.25 & 0.5 & 0.5 & 0.0 & 0.0 & 0.0 & 0.0 \\p_{{tilde}} & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\p_{{avg}} & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_{{avg}}) & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\\nabla f(x_{{tilde}}) & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\end{split}\]
print(
"Did we guess the right closed form of S?",
np.allclose(S_guess_eval, S_sol.matrix, atol=1e-4),
)
Did we guess the right closed form of S? True
Symbolic calculation#
Assemble the RHS of the proof.
interp_scalar_sum = pf.Scalar.zero()
for x_i, x_j in itertools.product(ctx_prf.tracked_point(f), ctx_prf.tracked_point(f)):
if lamb(x_i.tag, x_j.tag) != 0:
interp_scalar_sum += lamb(x_i.tag, x_j.tag) * f.interp_ineq(x_i.tag, x_j.tag)
display(interp_scalar_sum)
\[\displaystyle 0+1/2*(f(x_{{avg}})-f(x_1)+\nabla f(x_{{avg}})*(x_1-x_{{avg}}))+1/2*(f(x_{{avg}})-f(x_2)+\nabla f(x_{{avg}})*(x_2-x_{{avg}}))+1/2*(f(x_1)-f(x_{{tilde}})+\nabla f(x_1)*(x_{{tilde}}-(x_1)))+1/2*(f(x_2)-f(x_{{tilde}})+\nabla f(x_2)*(x_{{tilde}}-(x_2)))\]
for x_i, x_j in itertools.product(ctx_prf.tracked_point(g), ctx_prf.tracked_point(g)):
if gamm(x_i.tag, x_j.tag) != 0:
interp_scalar_sum += gamm(x_i.tag, x_j.tag) * g.interp_ineq(x_i.tag, x_j.tag)
display(interp_scalar_sum)
\[\displaystyle 0+1/2*(f(x_{{avg}})-f(x_1)+\nabla f(x_{{avg}})*(x_1-x_{{avg}}))+1/2*(f(x_{{avg}})-f(x_2)+\nabla f(x_{{avg}})*(x_2-x_{{avg}}))+1/2*(f(x_1)-f(x_{{tilde}})+\nabla f(x_1)*(x_{{tilde}}-(x_1)))+1/2*(f(x_2)-f(x_{{tilde}})+\nabla f(x_2)*(x_{{tilde}}-(x_2)))+1/2*(g(p_{{tilde}})-g(p_1)+u_{{tilde}}*(p_1-p_{{tilde}}))+1/2*(g(p_{{tilde}})-g(p_2)+u_{{tilde}}*(p_2-p_{{tilde}}))+1/2*(g(p_1)-g(p_{{avg}})+\nabla g(p_1)*(p_{{avg}}-(p_1)))+1/2*(g(p_2)-g(p_{{avg}})+\nabla g(p_2)*(p_{{avg}}-(p_2)))\]
RHS = interp_scalar_sum - S_guess
display(RHS)
\[\displaystyle 0+1/2*(f(x_{{avg}})-f(x_1)+\nabla f(x_{{avg}})*(x_1-x_{{avg}}))+1/2*(f(x_{{avg}})-f(x_2)+\nabla f(x_{{avg}})*(x_2-x_{{avg}}))+1/2*(f(x_1)-f(x_{{tilde}})+\nabla f(x_1)*(x_{{tilde}}-(x_1)))+1/2*(f(x_2)-f(x_{{tilde}})+\nabla f(x_2)*(x_{{tilde}}-(x_2)))+1/2*(g(p_{{tilde}})-g(p_1)+u_{{tilde}}*(p_1-p_{{tilde}}))+1/2*(g(p_{{tilde}})-g(p_2)+u_{{tilde}}*(p_2-p_{{tilde}}))+1/2*(g(p_1)-g(p_{{avg}})+\nabla g(p_1)*(p_{{avg}}-(p_1)))+1/2*(g(p_2)-g(p_{{avg}})+\nabla g(p_2)*(p_{{avg}}-(p_2)))-(1/alpha*3*\|x_0-x_{{tilde}}-alpha*3/4*(\nabla f(x_1)+u_1+\nabla f(x_2)+u_2)\|^2+alpha/3*\|u_0-u_{{tilde}}+3/4*(\nabla f(x_1)+u_1+\nabla f(x_2)+u_2)\|^2+alpha/16*(0+\|\nabla f(x_1)+u_1-(\nabla f(x_1)+u_1)\|^2+\|\nabla f(x_1)+u_1-(\nabla f(x_2)+u_2)\|^2+\|\nabla f(x_2)+u_2-(\nabla f(x_1)+u_1)\|^2+\|\nabla f(x_2)+u_2-(\nabla f(x_2)+u_2)\|^2))\]
Assemble the LHS of the proof
x_avg = ctx_prf["x_{{avg}}"]
u_avg = ctx_prf["u_{{avg}}"]
p_avg = ctx_prf["p_{{avg}}"]
p_tilde = ctx_prf["p_{{tilde}}"]
perf_metric = (
f(x_avg)
- f(x_tilde)
+ g(p_tilde)
- g(p_avg)
+ u_tilde * x_avg
- u_tilde * p_tilde
- u_avg * x_tilde
+ u_avg * p_avg
)
LHS = perf_metric - 1 / (alpha * (N + 1)) * (
(x_0 - x_tilde) ** 2 + alpha**2 * (u_0 - u_tilde) ** 2
)
diff = LHS - RHS
display(diff)
\[\displaystyle f(x_{{avg}})-f(x_{{tilde}})+g(p_{{tilde}})-g(p_{{avg}})+u_{{tilde}}*x_{{avg}}-u_{{tilde}}*p_{{tilde}}-u_{{avg}}*x_{{tilde}}+u_{{avg}}*p_{{avg}}-1/alpha*3*(\|x_0-x_{{tilde}}\|^2+alpha^2*\|u_0-u_{{tilde}}\|^2)-(0+1/2*(f(x_{{avg}})-f(x_1)+\nabla f(x_{{avg}})*(x_1-x_{{avg}}))+1/2*(f(x_{{avg}})-f(x_2)+\nabla f(x_{{avg}})*(x_2-x_{{avg}}))+1/2*(f(x_1)-f(x_{{tilde}})+\nabla f(x_1)*(x_{{tilde}}-(x_1)))+1/2*(f(x_2)-f(x_{{tilde}})+\nabla f(x_2)*(x_{{tilde}}-(x_2)))+1/2*(g(p_{{tilde}})-g(p_1)+u_{{tilde}}*(p_1-p_{{tilde}}))+1/2*(g(p_{{tilde}})-g(p_2)+u_{{tilde}}*(p_2-p_{{tilde}}))+1/2*(g(p_1)-g(p_{{avg}})+\nabla g(p_1)*(p_{{avg}}-(p_1)))+1/2*(g(p_2)-g(p_{{avg}})+\nabla g(p_2)*(p_{{avg}}-(p_2)))-(1/alpha*3*\|x_0-x_{{tilde}}-alpha*3/4*(\nabla f(x_1)+u_1+\nabla f(x_2)+u_2)\|^2+alpha/3*\|u_0-u_{{tilde}}+3/4*(\nabla f(x_1)+u_1+\nabla f(x_2)+u_2)\|^2+alpha/16*(0+\|\nabla f(x_1)+u_1-(\nabla f(x_1)+u_1)\|^2+\|\nabla f(x_1)+u_1-(\nabla f(x_2)+u_2)\|^2+\|\nabla f(x_2)+u_2-(\nabla f(x_1)+u_1)\|^2+\|\nabla f(x_2)+u_2-(\nabla f(x_2)+u_2)\|^2)))\]
pf.pprint_str(
diff.repr_by_basis(
ctx_prf,
sympy_mode=True,
resolve_parameters={"alpha": alpha_value, "R": R_value},
)
)
\[\displaystyle \displaystyle 0\]
With the verified closed form expression, we have verified the below for fixed \(N\)#
\[\begin{align*}
&\mathcal{L}(\bar{x}^N, \tilde{u}) - \mathcal{L}(\tilde{x}, \bar{u}^N)
- \frac{1}{\alpha (N+1)} \left( \|x^0 - \tilde{x}\|^2 + \alpha^2 \|u^0 - \tilde{u}\|^2 \right) \\
&= \frac{1}{N} \sum_{k=1}^N
\Big( f(\bar{x}^N) - f(x^k) +
\big\langle \tilde{\nabla} f(\bar{x}^N), x^k - \bar{x}^N \big\rangle \Big)
+ \frac{1}{N} \sum_{k=1}^N
\Big( f(x^k) - f(\tilde{x}) +
\big\langle \tilde{\nabla} f(x^k), \tilde{x} - x^k \big\rangle \Big)\\
& + \frac{1}{N} \sum_{k=1}^N
\Big( g(p^k) - g(\bar{p}^N) +
\big\langle u^k, \bar{p}^N - p^k \big\rangle \Big)
+ \frac{1}{N} \sum_{k=1}^N
\Big( g(\tilde{p}) - g(p^k) +
\big\langle \tilde{u}, p^k - \tilde{p} \big\rangle \Big) \\
& + \frac{1}{\alpha (N+1)}
\left(
\left\| x^0 - \tilde{x} - \frac{\alpha (N+1)}{2N} \sum_{k=1}^N v^k \right\|^2
+ \alpha^2
\left\| u^0 - \tilde{u} - \frac{N+1}{2N} \sum_{k=1}^N v^k \right\|^2
\right) \\
& + \frac{\alpha}{2N^2}
\sum_{k=1}^N \sum_{l=1}^{k-1}
\|v^k - v^l\|^2
\end{align*}\]
holds, where we denote \(v^k = \tilde{\nabla} f(x^k) + u^k\).